Lets get critical
Before getting to the core of this chapter, the basic conditions for the good quality of the selected radiological landmarks should be specified
In order to be perfectly valid, a landmark, used for tracing and/or superimpositions, must be all together :
- fixed,
- located in a stable zone, on the median Plane (as close as possible or projected on it)-
- easily spotted or easily constructed,
- have a real physiological value, with regard to the growth of the skeleton.
Practically,
In order, for a landmark (cephalometric point) to be validly used in a physiological study of skeletal cranio-facial growth, it must be located :
- either in the center of the "skeletal piece", the "territory", or the "skeletal ensemble" analyzed,
- or at their common borders (sutures),
- outside of an active area of superficial periosteum apposition or resorption (which is not the case for most of the points of the Conventional Analyses).
In order to be perfectly valid, a landmark, used for tracing and/or superimpositions, must be all together :
- fixed,
- located in a stable zone, on the median Plane (as close as possible or projected on it)-
- easily spotted or easily constructed,
- have a real physiological value, with regard to the growth of the skeleton.
Practically,
In order, for a landmark (cephalometric point) to be validly used in a physiological study of skeletal cranio-facial growth, it must be located :
- either in the center of the "skeletal piece", the "territory", or the "skeletal ensemble" analyzed,
- or at their common borders (sutures),
- outside of an active area of superficial periosteum apposition or resorption (which is not the case for most of the points of the Conventional Analyses).
|
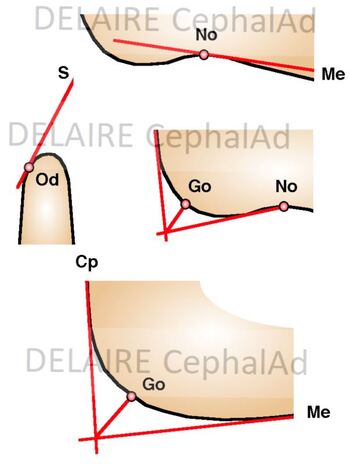
The points located at the level of a membrane suture which is a growth site have a great physiological value. It is the same for those located on nerve paths ie entry orifices or other specific points.
It must be precised that points located at the level of a skeletal curve are difficult to locate accurately. Whenever possible they will be "built" from lines tangent to the most convex or most concave point or at the point of intersection of the bisector of the angle formed by the tangents to the elements on either side of the curvature. (see right) |
Why classical radiological landmarks are questionnable ?
|
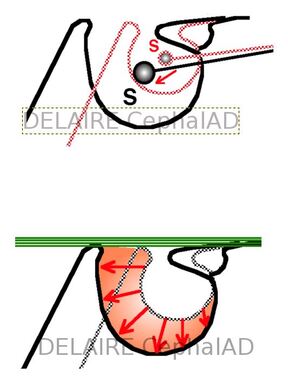
S point
In the course of the general growth the sella turcica expands. The S Point, located in its middle, moves backwards and downwards. This lowering reduces the S-N-A angle). On contrary the roof of the sella remains stable in time. This roof conforms under the influence of the aponeurotic intra-cranial tensor system of the base and its conformation is therefore regulated by dynamic factors). The development of the whole cavity results only from the expansion of the hypophyseal gland, which is very variable. depending on the subject) |
|
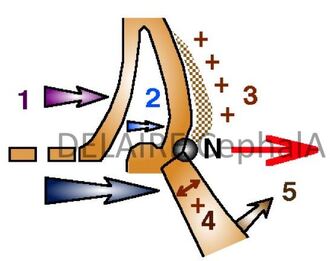
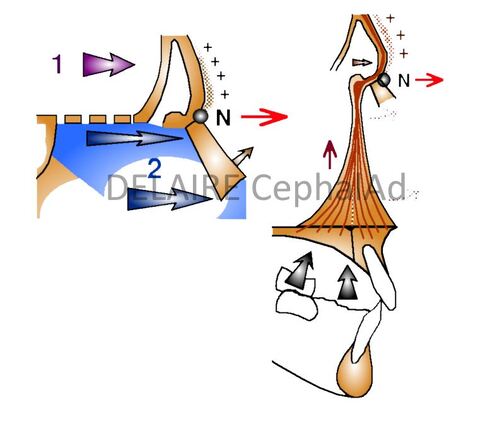
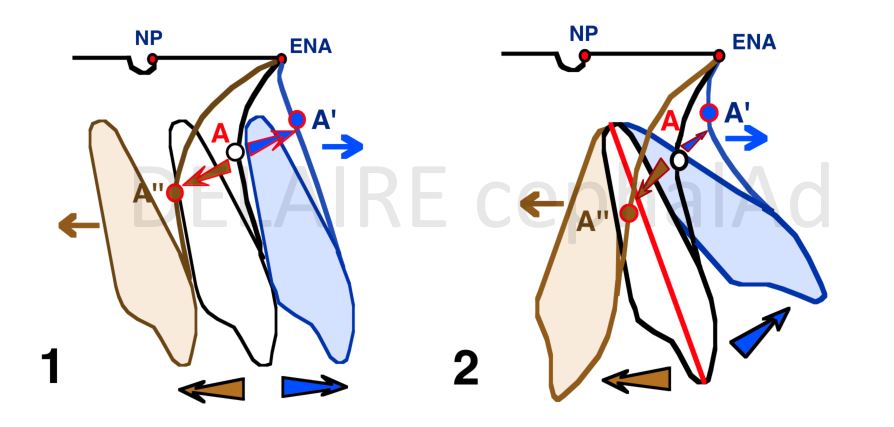
N point Its variability, in the sagittal sense, is extreme (depending on individuals, sex, population, age) this spontaneously and possibly also under the influence of certain Orthopaedic treatments. It is located at the most anterior part of the fronto-nasal suture and at the junction of the external cortex of the frontal bone and the nasal bones. Its location therefore depends on the development of these two skeletal elements. In a sagittal aspect it position depends on (A) : -1 2 the advancement of the frontal bone, and more specifically the anterior cortical of this bone. - 3 the thickening of this anterior cortical, - 4 the advancement and sagittal development of the nasal bones, - 5 the straightening of the nasal ridge The agents of thes movements being (B) : - 1 the development of frontal lobes of the brain, - 2 the expansion os the cartilaginous mesethmoid, - the occlusal forces araising from the anterior and lateral and lateral part of the upper dental arches, - possibly, orthopedic treatments... |
What has to be kept in mind is that N is not a facial point. N being located at the level of a membranous suture, this assures a certain validity, but only for the vertical developments of the facial skeleton, in which the naso frontal suture actively participates).
N must therefore be retained, but exclusively for measurements concerning the vertical dimensions of the facial skeleton.
|
A point
The Position of A varies a lot upon of the evolution of the dentition, and after their complete eruption upn the position and orientation of the upper central incisors. During the eruptive period and until these teeth are fully erupted, bone resorption usually occurs, the resulting recoil of A can be as much as 1 millimeter). A is a fundamentally a "Alveolar" point. In no case can it be used as a reference point to study the sagittal development of the maxilla. |
|
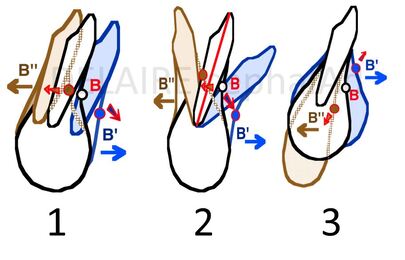
B point The position of B varies a lot depending on the evolution of the dentition and especially on the gressions (1) (pro or retro-alveolia), versions (2) (vestibulo or palato-version) and/or extrusions (3) (or intrusions) of the lower incisors. In fact, the main sagittal variations of B are due to the mandibular auto rotations (%). These auto rotations are depending on many factors : facial typology, muscular tonus, mouth breathing, volume of the tongue etc... B is an Alveolar point which position depends more on the situation and orientation of the lower incisors and mandibular rotations than on the development of the mandible. The biggest diagnostic errors have thus be committed using only the value of the SNA, SNB, and ANB angles. This has been the case, in particular for some Class III with huge anterior vertial excess falsely considered as Class II and treated as such. |
|
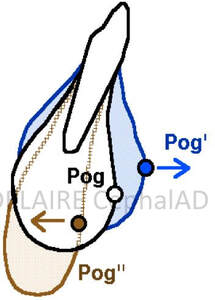
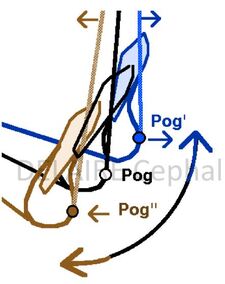
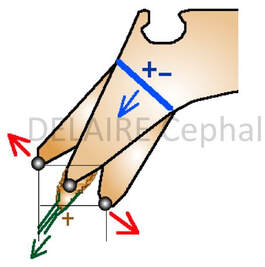
Pogonion (Pog) point
Pog is, theoretically, "the most anterior point of the mandibular symphyse" meaning the mandible itself. But the sagittal and vertical location of Pog varies greatly with the thickness of the symphysis, the degree of mandibular rotation, and the method of location. Examples of Pog Position Variations (Sagittal and Vertical) depending on the degree mandibular rotations ( and same mandible size) (%%).
Pog is a more a symphysis point than a mandibular one. Because of the great variations in shape, dimensions and position of the symphysis, it cannot, on its own, be used to accurately measure any mandibular dimensions and /or mandibular "growing. |
|
Basion (Ba) point
Ba does not have the fixed and stable position that the classics give him. In fact, its sagittal and vertical situation does not only depend on the growth activity of the spheno-occipital synchondrosis, but also on the orientation of the basilar apophysis of the occipital and on the ossification of of the ligaments that are inserted ont it. According to the ossification of the top of the odontoid and occipito-odonto-atloid Ligaments, the aspects of the basion region can be very different. |
|
FRANKFURT plan
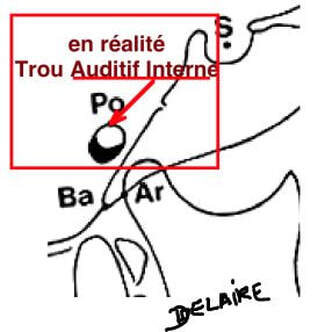
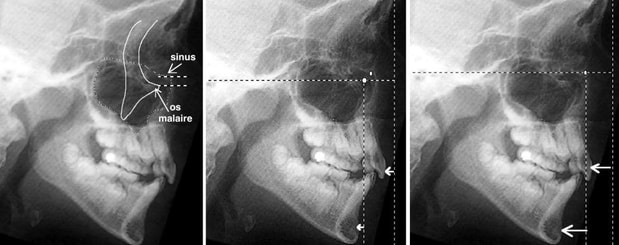
The Frankfurt plan is the fundamental reference in anthropology. It is traced from the Poron (Po) point, superior aspect of the image of the external ear canal, to the orbitale point (Or), lower border of the left orbit. When taking profile teleradiographs, the frankfurt plan guides the radiologists to properly orient the head of their patients. It is therefore not surprising that almost all first cephalometric analyses have chosen this planas both the orientation plan and the reference plan. This is especially true for the Tweed methods, Downs, Wylie, Mac Namara, Bimler, and even (but in association with other references) Broadbent, de Coster, Ricketts. But this plane asks some questions. Porion is often badly located on the internal ear canal instead of the external one. (%1) Orbitale is often badly located (%2). It is often located much too high, at the level of the maxillary sinus roof (which upper-middle part normally exceeds the orbital floor). Depending on its location, the facial anomalies analyzed thanks to vertical lines trace perpendicular to the Frankfurt plan can be very different. And angular projections can exagerate the initial imprecision. |
|
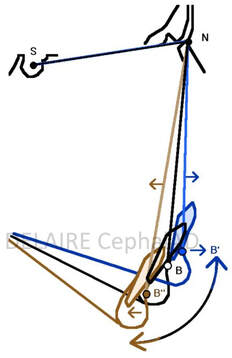
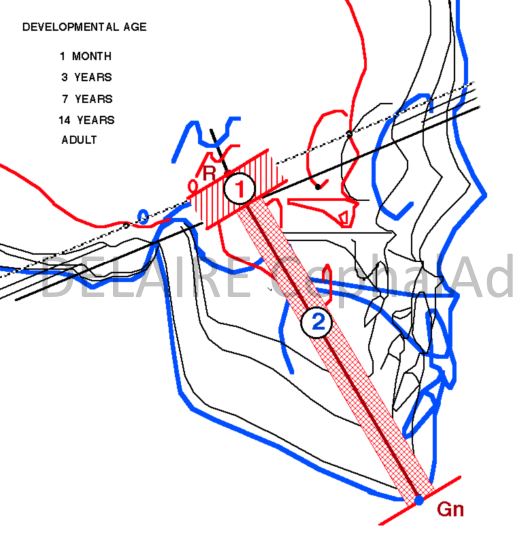
Broadbent R point
The R (registration point) is drawn in the middle of the perpendicular lowered from the centre of the saddle turcica on the Nasion-Bolton line, in the supposedly most stable part of the Base of the skull (the body of the sphenoid). The R Point does not have the indispensable Physiological Value for the Study of the Development of the face. In fact, the lines that start from it, for example the R-Gn Line, have 2 different segments: - the first (1) corresponds to the lower half of the body of the sphenoid, - the other (2) to the face. Unfortunately the elongation of R-Gn, during growth, is therefore the Sum of the 2 "basal" and "facial" increments. |
FINALLY
in total, most of the points used in traditional cephalometric analyses are :
- difficult to locate accurately,
- unstable
- almost all of them, without real physiological value.
The difficulties of their locating, the instability, and the insufficient physiological value of the landmarks of conventional analyses puts obviously in cause the stability and validity of the lines that unite them and the angles that they form between them.
May be classical cephalometries can only show what we want to see ... instead of showing the physiological and anatomical reality.
in total, most of the points used in traditional cephalometric analyses are :
- difficult to locate accurately,
- unstable
- almost all of them, without real physiological value.
The difficulties of their locating, the instability, and the insufficient physiological value of the landmarks of conventional analyses puts obviously in cause the stability and validity of the lines that unite them and the angles that they form between them.
May be classical cephalometries can only show what we want to see ... instead of showing the physiological and anatomical reality.
end of section